|
تنگ طه
وبلاگي شامل مطالب آموزشي دوره ابتدايي و مطالبي درباره روستاي تنگ طه
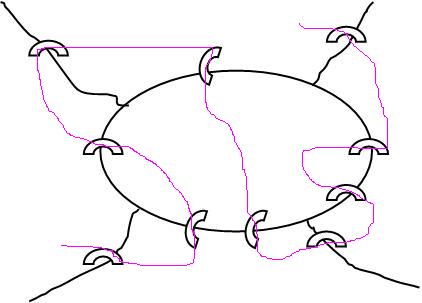
1 - شهري در وسط دو رود كه دور شهر را احاطه نموده و از دو طرف خارج شده اند به صورت زير قرار دارد . يك پستچي مي خواهد از يك طرف شهر شروع به توزيع نامه ها نمايد و از طرف ديگر خارج شود . اما اين راهپيمايي او چند شرط دارد . اول اينكه او حتما بايد از روي تمام پلها عبور نمايد و از روي هر پل هم فقط يكبار مي تواند عبور كند و در ضمن مسير او بايد كوتاهترين مسير ممكن باشد . محل ورود و خروج او هم مهم نيست .
مطابق شكل زير :
2 - فروشنده دوره گردي دو ظرف 20 ليتري و 30 ليتري روغن دارد . دو نفر براي خريد روغن به او مراجعه مي نمايند و تقاضاي دو ليتر روغن مي نمايند . اما فروشنده ظروف پيمانه خود را به همراه ندارد . ظرفهاي آن دو نفر نيز 3 ليتري و 4 ليتري مي باشد . اين فروشنده چگونه مي تواند با كمترين تعداد جا به جايي به هر كدام دو ليتر روغن بدهد ؟ مطابق جدول زير
3 - از عددي يك ، ششم سه، چهارم خودش و نصف خودش را كم نموديم . عدد 9 حاصل آمد . عدد اوليه چقدر بوده است ؟
ابتدا يك ، ششم سه، چهارم را حساب مي كنيم كه مي شود ، سه ، بيست وچهارم يا يك ، هشتم حالا معادله را نوشته و آن را حل مي نماييم .
4 - مساحت مثلث قائم الزاويه اي با مساحت يك دايره برابر است . محيط دايره برابر طول يك ضلع زاويه قائمه مثلث و قطر دايره برابر 6 سانتي متر مي باشد . طول ضلع ديگر زاويه قائمه مثلث را پيدا نماييد . طول ضلع ديگر برابر شعاع دايره و برابر 3 سانتي متر مي باشد . چون براي مساحت مثلث داريم : 2 ÷ ضلع ديگر × (3/14 × 2 × شعاع ( محيط دايره )) حال اگر همين رابطه را ساده نماييم ضرب در 2 و تقسيم بر 2 حذف شده و مي ماند : 3/14 × ضلع ديگر × شعاع كه اين همان مساحت دايره است كه به جاي شعاع ، ضلع ديگر مثلث را قرار داده ايم . پس هر گاه مساحت دايره با مساحت مثلث برابر باشد و قاعده مثلث برابر محيط دايره باشد ، ارتفاع مثلث برابر شعاع دايره خواهد بود .
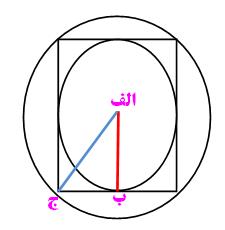
5 - مساحت دايره محيطي يك مربع چه كسري از مساحت دايره محاطي آن مي باشد ؟
اگر دو شعاع دايره محاطي و محيطي را به صورت شكل روبه رو رسم نماييم يك مثلث قائم الزاويه حاصل مي گردد كه وتر آن شعاع دايره محيطي و يك ضلع زاويه قائمه آن هم شعاع دايره محاطي مي باشد . اندازه ضلع ديگر مثلث نيز برابر شعاع دايره محاطي مي باشد زيرا در مربع زاويه قطرها با ضلع مربع برابر 45 درجه مي باشد و چون در مثلث دو زاويه 45 درجه مي شود بنابراين مثلث متساوي الساقين است . حال براي پيدا كردن مساحت بايد مجذور شعاع را در 3/14 ضرب نمود كه مجذور شعاع آبي رنگ برابر است با دو برابرمجذور شعاع قرمز رنگ ( طبق قاعده فيثاغورث ) پس مساحت دايره محيطي دو برابر دايره محاطي مي شود .
6 - مي خواهيم مثلثهاي قائم الزاويه اي رسم نماييم كه اندازه همه اضلاع آنها عدد صحيح باشد . اندازه اضلاع چند نمونه را پيدا نماييد . ابتدا از ساده ترين آنها استفاده مي كنيم . اندازه هايي كه در گذشته براي رسم زاويه قائمه از آن استفاده مي شده يعني 3 و 4 و 5 كه مجذور وتر و مجذور دو ضلع زاويه قائمه برابر 25 مي باشد . حال اگر همين اندازه ها را در 2 ضرب نماييم باز مثلث قائم الزاويه خواهد شد . يعني 6 و 8 و 10 كه مجذور وتر و دو ضلع ديگر برابر هم و مساوي 100 خواهد شد . اگر همين اندازه ها را در 3 ضرب نماييم مي شود 9 و 12 و 15 كه باز مجذور وتر و دو ضلع ديگر برابر و مساوي 225 مي شود پس باز مثلث قائم الزاويه خواهد بود . اين اندازه ها را در هر عددي ضرب نماييم ، باز مثلث حاصل قائم الزاويه خواهد بود . راه ديگر مي دانيم كه اختلاف مجذور اعداد طبيعي به ترتيب دو تا مي باشد و اختلاف دو مجذور متوالي هميشه عددي فرد بوده و برابر است با خود عدد به علاوه عدد قبل از خود . حال مي توانيم اعدادي پيدا نماييم كه اولا مجذور كامل باشند و فرد بوده و بعد هم از مجموع دو عدد متوالي حاصل آيد كه ازدو عدد متوالي عدد بزرگتر اندازه وتر و عدد كوچكتر اندازه يك ضلع زاويه قائمه و جذر اختلاف نيز ضلع ديگر است . مطابق اين قوانين اولين عدد 9 است كه از مجذور كامل است و فرد مي باشد و از مجموع دو عدد 4 و 5 حاصل مي گردد . و 4 و 5 و جذر 9 كه 3 مي شود هم سه ضلع آن هستند . عدد بعدي كه طبق اين قاعده مي يابيم 25 است كه از مجموع 12 و 13 حاصل مي شود . و اعداد مثلث 12 و 13 و مجذور 25 كه 5 است مي شوند . عدد بعدي 49 است كه از مجموع 24 و 25 حاصل مي آيد و اعداد مثلث 24 و 25 و مجذور 49 كه 7 مي باشد هستند و به همين ترتيب اعداد ديگر را نيز مي توان يافت .
7 - شخصي از فردي كه پول خود را ربا مي داد مقدار200000 تومان پول به ربا گرفت و قرار شد درمدت 20 ماه پول را با سودش برگرداند و قسطهاي او نيز به ترتيب براي ماه اول 2 در صد كل پول و براي ماه هاي بعدي هرماه به اندازه يك برابر و نيم ماه قبل مي باشد . شخص ربا گيرنده بسيار خوشحال شد و با خود فكر كرد مرد بيچاره حساب و كتاب بلد نيست حتي پول خودش هم گيرش نمي آيد تا چه رسد كه سود هم بكند . اما در پايان ديد كه اشتباه فكر كرده است . مجموع پولي كه اين شخص بابت اين پول بايد به ربا دهنده بپردازد چقدر مي باشد ؟ را با رابطه تصاعد هندسي مي توان حساب نمود . جمله اول را پيدا مي كنيم . جمله اول 2 در صد 200000 تومان يا 2000 تومان مي باشد . قدر نسبت هم كه 1/5 مي باشد و تعداد جمله ها هم كه 20 مي باشد . و با محاسبه مبلغي كه ربا گيرنده بايد بپردازد يعني مبلغ 13297026 تومان ميزان سادگي او و سطحي نگري او مشخص مي گردد . 8 - فردي از انسان نيكوكاري مبلغ 4095000 تومان وام قرض الحسنه گرفت و قرار شد وام را ماهيانه ظرف مدت يك سال بپردازد و چون وضعيت او خوب نبود ، قرار شد بازپرداخت او به صورت پلكاني باشد به اين ترتيب كه هر مقدار ماه اول پرداخت نمود ماه بعد دوبرابر آن بپردازد و ماههاي بعدي هم به همين ترتيب هر ماه دو برابر ماه قبلي . او بايد در هر ماه چقدر بپردازد ؟ با استفاده از تصاعد هندسي مي توان به راحتي جواب را پيدا نمود . مجموع جملات برابر است با كل مبلغ وام كه 4095000 مي باشد و قدر نسبت هم برابر 2 مي باشد و تعداد جملات هم برابر اقساط كه 12 است مي باشد . در نتيجه جمله اول يا قسط اول برابر 1000 تومان است . قسط دوم 2000 و قسط سوم 4000 قسط چهارم 8000 و قسط پنجم 16000 و قسط ششم 32000 و قسط هفتم 64000 و قسط هشتم 128000 و قسط نهم 256000 و قسط دهم 512000 و قسط يازدهم 1024000 و قسط آخر 2048000 تومان مي باشد .
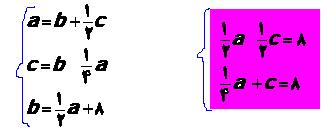
9 - سه عدد را طوري پيدا نماييد كه عدد بزرگ برابر عدد متوسط و نصف عدد كوچك باشد و عدد كوچك برابر عدد متوسط منهاي ربع عدد بزرگ باشد و عدد متوسط برابر نصف عدد بزرگ به علاوه 8 باشد . سه عدد را به ترتيب aو b و c مي ناميم و معادله آن را مي نويسيم . در معادله 1 و 2 به جاي b مقدار آن را قرار مي دهيم و دو معادله به اين صورت در مي آيند : و اگر معادله اول را در دو ضرب نماييم و معادله را حل كنيم
مقدار a = 32 و مقدار b = 24 و c = 16 به دست مي آيد .
نظرات شما عزیزان:
آخرین مطالب آرشيو وبلاگ پيوندها تبادل لينك هوشمند نويسندگان
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
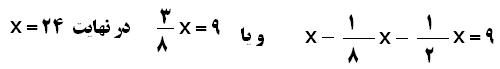

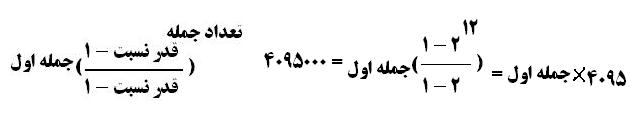

 آمار
وب سایت:
آمار
وب سایت: